Tufte’s Beautiful Evidence, Chapter 3: Links and Causal Arrows: Ambiguity in Action

Posted on | July 30, 2006 | Comments Off

Welcome to my thoughts on chapter 3 of Tufte’s Beautiful Evidence. If you haven’t yet, you can read what I thought of Chapters 1 and 2.

As an information architect and interaction designer, I’ve had my share of trafficking in boxes and arrows — diagrams of schemes, systems, processes, and flows, commonly depicted as elements connected through lines. So it was with great anticipation that I approached the third chapter, which begins with this diagram:

The chapter gets off to a good start, with this informative diagram, and Tufte serves the reader well in his assessment of its strengths and weaknesses. The primary thrust of this chapter is that linking elements in diagrams, typically represented as lines or arrows, are too often ambiguous in meaning; or, even worse, different links in a diagram, which might appear identical, might have different meaning (i.e., one line might mean “influenced by” as you see in the diagram above, while another line might mean simply “related to”, etc. etc.)

The chapter starts losing focus when showcasing Ad Reinhardt’s brilliant cartoon “How to Look at Modern Art in America.” In part because, though a fun illustration, the cartoon has very little to do with the thrust of Tufte’s thesis. Also, because I think Tufte takes the drawing too seriously, seeing it as a weighty condemnation of certain art practices. I find it hard to discern Reinhardt’s specific point of view, but in some ways that doesn’t matter. It’s a cartoon. Enjoy it as such.

The Mark Lombardi drawing brings Tufte back on focus, but sadly he spends only half a page on his work. Yet Lombardi, and the influence he draws from, the sociogram, showcase an essential expression of the link and causal arrow — how people are connected to one another through various relationships. (Also think: family trees, or, if you want to get more involved, anthropological kinship diagrams.)

Such diagrams are pretty easy for people to appreciate, yet Tufte doesn’t use these kinds of diagrams to dig into his analysis. Instead, he goes on about cladograms (which depict evolutionary development), Feynman diagrams, and Italian drawings from the 15th and 16th Century. It’s as if he’s purposefully obfuscatory — perhaps with some desire to deonstrate his breadth? I mean, the horsey made all up of annotated lines is, frankly, a useless illustration. And yet it gets two full pages devoted to it.

The one exception to this is the diagram depicting the spread of SARS, which Tufte rightly displays as an exemplar, even though it’s “design” is *extremely* basic.

I found this chapter to be perhaps the most disappointing so far, because it’s a subject so close to my interests. Whether website architecture diagrams, social network diagrams, or conceptual models like mind maps, boxes and circles connected by various lines is a fundamental tool in the strategic designer’s box.

Thinking of links and causal arrows brings me to a conceptual model Jesse and I developed for a client, a bank. Here is one small section of the model (which has links to other parts that you’ll just have to ignore).

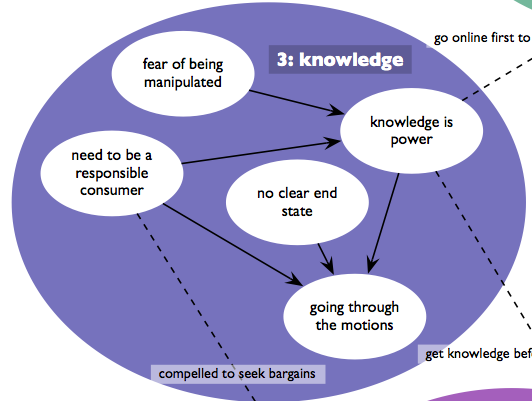
Thematic Model

We called this the thematic model, because it addressed themes that emerged from our user research observations. What for me was interesting about this bubble was the story it told:

People, when acquiring financial products and services (like checking accounts, loans, etc.), have a fear of being manipulated. That leads them to seek knowledge, because knowledge is power. They also have a sense of what it means to be a responsible consumer, which means to compare options across providers. The thing is, these folks were unable to articulate an end state (the precise product and service, with its fees, percentages, etc.), and when you combined these three concepts, you ended up with someone who, when shopping for financial products, just goes through the motions.

Now, what Tufte would point out, and I think he’d be right, is that our arrows are woefully ambiguous. The drawing requires explanation — it is in no way self-evident, and a legend wouldn’t help, because all the lines look the same. BUT, and I think this is important, I can think of no more a compact way of presenting this finding of ours, and I think the visual does compel.

Anyway, Tufte really only scratches the surface of the discussion here, getting distracted by diagrams either too technical or too archaic to be of general use. Maybe Dan’s book can help those us needing more applicable examples?

Comments

Comments are closed.

peterme.com

Links, thoughts, and essays from Peter Merholz

Tufte’s Beautiful Evidence, Chapter 3: Links and Causal Arrows: Ambiguity in Action

Comments

Recent Comments

Hello

Archives

peterme.com

Links, thoughts, and essays from Peter Merholz

Tufte’s Beautiful Evidence, Chapter 3: Links and Causal Arrows: Ambiguity in Action

Comments

Recent Comments

Tags

Hello

Archives